
Biznes
Müəssisə — mülkiyyət formasından asılı olmayaraq ictimai tələbatın ödənilməsi və mənfəət əldə edilməsi məqsədilə məhsul istehsal edən, satan, müvafiq iş və xidmətlər yerinə yetirən hüquqi şəxs olan müstəqil təsərrüfat subyektidir.
Müəssisə termini aşağıdakı üç termini özündə əks etdirir:
Maşın və bu kimi istehsal ünsürlərini çalışdırmaq, yəni, onlara iş gördürmək üçün bir vasitədir;
Müxtəlif iş və fəaliyyətlərin yerinə yetirildiyi yer, iş yeri;
Maddi və fəal elementlərdən (texnika, sərmayəvə işçilər) əmələ gələn bir istehsal vahididir.
Müəssisə anlayışının hər üç tərifində fəal, yəni istehsaledici bir hərəkətdə və fəaliyyətdə olma görünür. Ancaq birinci yalnız texniki, ikinci və üçüncüsü kütləyə (xalqa) və texnikaya aid xüsusiyyətlərə malikdir.
Birinci mənada alət və maşın kimi texniki vasitələrdən istifadə, onlara iş gördürmə anlaşıldığı kimi, bir dükan, mağaza, fabrik və s. kimi də iş yerlərini fəaliyyətdə olub-olmadığı da düşünülür. Müəssisə sözünün bu anlamı dinamik bir xüsusiyyətə malikdir.
İkinci mənada fabrik, büro, dəftərxana, ticarətxana və bu kimi terminlərin ifadə etdiyi işlərin göründüyü kimi yerlər müəyyənləşir ki, bu da, müəssisənin statik bir məna daşıdığını göstərir.
Üçüncü mənada isə elmi hərəkətlərin olduğu yer deyil, bu hərəkətləri görmək üçün müəyyənləşdirilmiş təşkilat başa düşülür.
== Müəssisənin quruluşu ==
Müəssisə — ölkə iqtisadiyyatının ilkin halqası olub, müəyyən mülkiyətə və kollektiv əməyə əsaslanan ictimai tələbatı ödəmək və mənfəət əldə etmək məqsədilə məhsul istehsal edən, iş və xidmətlər göstərən, istehsal-texniki, təşkilati və iqtisadi vəhdətə malik olan hüquqi şəxs statuslu istehsal təsərüfat vahididir.

Davamlılıq tənliyi
Davamlılıq tənliyi, axdığı boru içərisindəki duruların (mayelərin) axını, onu qoruyub saxlayan bir tənlikdir. Kütlə, enerji, impuls, elektrik yükü və digər təbii miqdarlar lazımi şəraitdə saxlanıldığı üçün müxtəlif fiziki hadisələri davamlılıq tənliyi ilə təsvir etmək olar.
== Sıxılmış durular için davamlılıq tənliyi ==
ρ
1
⋅
V
1
⋅
A
1
=
ρ
2
⋅
V
2
⋅
A
2
{\displaystyle \rho _{1}\cdot \mathbf {V} _{1}\cdot \mathbf {A} _{1}=\rho _{2}\cdot \mathbf {V} _{2}\cdot \mathbf {A} _{2}}
burada;
ρ
{\displaystyle \rho \,}
: Sıxlıq ,
V
{\displaystyle \mathbf {V} }
Durunun sürəti ,
A
{\displaystyle \mathbf {A} }
: Məhdud (Enkesit) vektorial sahədir .
== Sıxılmayan durular için davamlılıq tənliyi ==
V
1
⋅
A
1
=
V
2
⋅
A
2
{\displaystyle \mathbf {V} _{1}\cdot \mathbf {A} _{1}=\mathbf {V} _{2}\cdot \mathbf {A} _{2}}
burada;
V
{\displaystyle \mathbf {V} }
Durunun sürəti ,
A
{\displaystyle \mathbf {A} }
: Məhdud (Enkesit) vektorial sahədir .

Diofant tənliyi
Diofant tənliyi — adını e.ə III əsrdə yaşadığı təxmin edilən qədim yunan riyaziyyatçısı Diofantdan alan dəyişənləri və əmsalları tam ədəd olan tənlik. Diofant "Hesab" adlı yalnız 6 cildi günümüzə gəlib-çatan əsərində 130 tənliyi və onların həllini qeyd etmişdir.
== Xətti Diofant tənlikləri ==
Sadə xətti tənlikdə nümunələr aşağıdakı kimi verilə bilər;
Nümunə 1.1
x
+
y
=
1
{\displaystyle x+y=1}
Bu bərabərlikdə hər bir x qiyməti üçün tək bir y həlli var. (
y
=
1
−
x
{\displaystyle y=1-x}
).
Bu bərabərliyin həll çoxluğu;
(X, 1 − X) şəklindədir hər X ∈ Z üçün
Nümunə 1.2
x
+
2
y
=
1
{\displaystyle x+2y=1}
Bu dəfə x-in hər hansı bir tam ədəd ola bilməyəcəyi, lakin sadəcə tək ədəd ola biləcəyi görülür (
x
=
1
−
2
y
{\displaystyle x=1-2y}
).
Bu bərabərliyin həll çoxluğu;
(1-2y, y) şəklindədir hər y ∈ Z üçün
Nümunə 1.3
3
x
+
6
y
=
1
{\displaystyle 3x+6y=1}
Bu bərabərliyin həlli boş çoxluqdur. Hər
x
{\displaystyle x}
və
y
{\displaystyle y}
tam ədəd seçimi üçün bu tənliyin sol tərəfi həmişə 3-cü qüvvət olduğu halda sağ tərəfi heç vaxt 3-cü qüvvətdən ola bilməz.
=== Ümumi xətti Diofant tənliyi ===
a
x
+
b
y
=
c
{\displaystyle ax+by=c}
şəklindədir. Burada a, b və c tam əmsallar
x
{\displaystyle x}
və
y
{\displaystyle y}
tam ədəd dəyişənləridir.
== Digər nümunələr ==
=== Pifaqor teoremi ===
Ümumi bir nümunə Pifaqor tənliyidir (Bax: Pifaqor teoremi)
Nümunə 2.1.1
x
2
+
y
2
=
z
2
{\displaystyle x^{2}+y^{2}=z^{2}\,}
Burada
x
,
y
,
z
{\displaystyle x,y,z}
tam ədədləri düzbucaqlı üçbucağın kənar tərəflərini təmsil etdiyi üçün Pifaqor üçlüyü olaraq da adlandırılır.

Diyofantus tənliyi
Diofant tənliyi — adını e.ə III əsrdə yaşadığı təxmin edilən qədim yunan riyaziyyatçısı Diofantdan alan dəyişənləri və əmsalları tam ədəd olan tənlik. Diofant "Hesab" adlı yalnız 6 cildi günümüzə gəlib-çatan əsərində 130 tənliyi və onların həllini qeyd etmişdir.
== Xətti Diofant tənlikləri ==
Sadə xətti tənlikdə nümunələr aşağıdakı kimi verilə bilər;
Nümunə 1.1
x
+
y
=
1
{\displaystyle x+y=1}
Bu bərabərlikdə hər bir x qiyməti üçün tək bir y həlli var. (
y
=
1
−
x
{\displaystyle y=1-x}
).
Bu bərabərliyin həll çoxluğu;
(X, 1 − X) şəklindədir hər X ∈ Z üçün
Nümunə 1.2
x
+
2
y
=
1
{\displaystyle x+2y=1}
Bu dəfə x-in hər hansı bir tam ədəd ola bilməyəcəyi, lakin sadəcə tək ədəd ola biləcəyi görülür (
x
=
1
−
2
y
{\displaystyle x=1-2y}
).
Bu bərabərliyin həll çoxluğu;
(1-2y, y) şəklindədir hər y ∈ Z üçün
Nümunə 1.3
3
x
+
6
y
=
1
{\displaystyle 3x+6y=1}
Bu bərabərliyin həlli boş çoxluqdur. Hər
x
{\displaystyle x}
və
y
{\displaystyle y}
tam ədəd seçimi üçün bu tənliyin sol tərəfi həmişə 3-cü qüvvət olduğu halda sağ tərəfi heç vaxt 3-cü qüvvətdən ola bilməz.
=== Ümumi xətti Diofant tənliyi ===
a
x
+
b
y
=
c
{\displaystyle ax+by=c}
şəklindədir. Burada a, b və c tam əmsallar
x
{\displaystyle x}
və
y
{\displaystyle y}
tam ədəd dəyişənləridir.
== Digər nümunələr ==
=== Pifaqor teoremi ===
Ümumi bir nümunə Pifaqor tənliyidir (Bax: Pifaqor teoremi)
Nümunə 2.1.1
x
2
+
y
2
=
z
2
{\displaystyle x^{2}+y^{2}=z^{2}\,}
Burada
x
,
y
,
z
{\displaystyle x,y,z}
tam ədədləri düzbucaqlı üçbucağın kənar tərəflərini təmsil etdiyi üçün Pifaqor üçlüyü olaraq da adlandırılır.

Dreyk tənliyi
Dreyk tənliyi — qalaktikada bizimlə əlaqəyə girmək ehtimalı olan sivilizasiyaların sayını hesablamağa imkan verən riyazi formul.
Formul aşağıdakı kimidir:
N
=
R
⋅
f
p
⋅
n
e
⋅
f
l
⋅
f
i
⋅
f
c
⋅
L
{\displaystyle N=R\cdot f_{p}\cdot n_{e}\cdot f_{l}\cdot f_{i}\cdot f_{c}\cdot L}
burada,
N
{\displaystyle ~N}
— əlaqəyə girməyə hazır olan sivilizasiyaların sayı;
R
{\displaystyle ~R}
— il ərzində bizim qalaktikada yaranan ulduzların sayı;
f
p
{\displaystyle ~f_{p}}
— planetləri olan ulduzların xüsusi çəkisi;
n
e
{\displaystyle ~n_{e}}
— sivilizasiyanın yaranması üçün müvafiq şəraitə malik olan planetlərin və peyklərin sayı;
f
l
{\displaystyle ~f_{l}}
— müvafiq şəraitə malik olan planetdə həyatın yaranması ehtimalı;
f
i
{\displaystyle ~f_{i}}
— həyat olan planetdə şüurlu varlıqların yaranma ehtimalı;
f
c
{\displaystyle ~f_{c}}
— əlaqəyə hazır olan və əlaqəyə girmək istəyən şüurlu sakinlərə malik planetlərlə, şüurlu sakinləri olan planetlərin sayına nisbəti;
L
{\displaystyle ~L}
— bu sivilizasiyaların ömür müddəti.
Formul Kaliforniyanın Santa-Kruz Universitetinin astronomiya və astrofizika professoru Frenk Donald Dreyk tərəfindən 1960-cı ildə təklif olunmuşdur. Onun 1961-ci ildə ehtimal olunan rəqəmlər əsasında apardığı hesablama aşağıdakı kimi olmuşdur.
R = 10/il (ildə 10 ulduz yaranır)
fp = 0.5 (ulduzların yarısının planetləri var)
ne = 2 (sitemdə orta hesabla 2 planet həyat üçün yararlıdır)
fl = 1 (əgər həyatın yaranma ehtimalı varsa, o mütləq yaranır)
fi = 0.01 (həyatın şüurlu formayadək inkişaf etməsi ehtimalı – 1 %)
fc = 0.01 (sivilizasiyaların 1 %-i əlaqə yaratmaq imkanına malik olacaq və əlaqə qurmaq istəyəcək)
L = 10 000 il (texniki cəhətdən inkişaf etmiş sivilizasiya 10000 il mövcud olur)
Bu təxmini hesablamaya əsasən N = 10 × 0,5 × 2 × 1 × 0,01 × 0,01 × 10000 = 10.
Tənlikdəki göstəricilərdən yalnız
R
{\displaystyle ~R}
və
f
p
{\displaystyle ~f_{p}}
astronomiyanın indiki inkişaf səviyyəsində müəyyən qədər dəqiq müəyyənləşdirilə bilər. Digər göstəricilərin müəyyənləşdirilməsi mümkün olmadığından Dreyk tənliyi kəskin tənqidlərlə qarşılaşmışdır.

Koşi tənliyi
Koşi ötürmə tənliyi Optikada müəyyən bir şəffaf material üçün işığın sınma indeksi və dalğa uzunluğu arasında empirik əlaqə . Adını 1837-ci ildə təyin edən riyaziyyatçı Oqüsten Koşinin şərəfinə almışdır.
== Tənlik ==
Koşi tənliyinin ən ümumi forması
n
(
λ
)
=
A
+
B
λ
2
+
C
λ
4
+
⋯
,
{\displaystyle n(\lambda )=A+{\frac {B}{\lambda ^{2}}}+{\frac {C}{\lambda ^{4}}}+\cdots ,}
burada n sınma əmsalıdır, λ dalğa uzunluğu, A, B, C və s., tənliyi məlum dalğa uzunluqlarında ölçülmüş sındırma göstəricilərinə uyğunlaşdırmaqla material üçün müəyyən edilə bilən əmsallardır . Əmsallar adətən mikrometrlərdə vakuum dalğa uzunluğu (materialın daxilində olan λ/n kimi deyil) kimi λ üçün göstərilir.
Adətən, tənliyin ilk iki həddindən istifadə etmək kifayətdir:
n
(
λ
)
=
A
+
B
λ
2
,
{\displaystyle n(\lambda )=A+{\frac {B}{\lambda ^{2}}},}
burada A və B əmsalları tənliyin bu forması üçün xüsusi olaraq təyin edilir.
Ümumi optik materiallar üçün əmsallar cədvəli aşağıda göstərilmişdir:
işıq-maddə qarşılıqlı əlaqəni əsaslandıran Koşinin bu tənliyi sonradan yanlış olduğu məlum oldu. Xüsusilə, tənlik yalnız görünən dalğa uzunluğu bölgəsində normal dispersiya bölgələri üçün keçərlidir. İnfraqırmızı dalğalarda tənlik qeyri-dəqiq olur və anomal dispersiya bölgələrini təmsil edə bilmir. Buna baxmayaraq, onun riyazi sadəliyi onu bəzi tətbiqlərdə faydalı edir.
Zelmeyer tənliyi anomal dispersiv bölgələri əhatə edən və ultrabənövşəyi, görünən(400-700 nm dalğa uzunluqlu şüalar) və infraqırmızı spektrdə materialın sındırma indeksini daha dəqiq modelləşdirən Koşinin çalışmasının genişləndirilmiş formasıdır.

Laplas tənliyi
Laplas tənliyi riyaziyyatda və fizikada ikitərtibli xüsusi törəməli diferensial tənlikdir. Xüsusiyyətləri ilk dəfə Pyer Simon Laplas tərəfindən tətqiq edildiyinə görə onun adını daşıyır. Tənliyin yazılışı aşağıdaki kimidir:
∇
2
f
=
0
və ya
Δ
f
=
0
,
{\displaystyle \nabla ^{2}\!f=0\qquad {\mbox{və ya}}\qquad \Delta f=0,}
Burada
Δ
=
∇
⋅
∇
=
∇
2
{\displaystyle \Delta =\nabla \cdot \nabla =\nabla ^{2}}
Laplas operatoru,
∇
⋅
{\displaystyle \nabla \cdot }
divergensiya operatoru,
∇
{\displaystyle \nabla }
qradiyent operatoru və
f
(
x
,
y
,
z
)
{\displaystyle f(x,y,z)}
isə iki dəfə diferensiallana bilən həqiqi qiymətli funksiyadır. Belə ki, Laplas operatoru skalyar bir funksiyanı başqa skalyar funksiyaya inkas etdirir. Sağ tərəfdə
h
(
x
,
y
,
z
)
{\displaystyle h(x,y,z)}
funksiyası təyin olunarsa, onda Laplas tənliyi aşağıdaki kimi verilir:
Δ
f
=
h
.
{\displaystyle \Delta f=h.}
Buna Puasson tənliyi, Laplas tənliyinin ümumiləşdirilməsi deyilir. Laplas və Poisson tənlikləri eliptik xüsusi törəməli diferensial tənliklərin ən sadə nümunələridir. Laplas tənliyi, həmçiin Helmholtz tənliyinin xüsusi bir haldır. Laplas tənliyinin həllərinin ümumi nəzəriyyəsi potensial nəzəriyyə olaraq bilinir. Laplas tənliyinin həlli fizikanın bir çox sahələrində, xüsusən elektrostatikada, qravitasiya və maye dinamikasında mühüm əhəmiyyət daşıyan harmonik funksiyalardır.

Rikkati tənliyi
y
′
+
a
(
x
)
y
+
b
(
x
)
y
2
+
c
(
x
)
=
0
{\displaystyle y^{\prime }+a(x)y+b(x)y^{2}+c(x)=0}
(
∗
)
{\displaystyle (*)}
şəklində tənliyə Rikkati tənliyi deyilir. Rikkati tənliyi
b
(
x
)
=
0
{\displaystyle b(x)=0}
olduqda xətti,
c
(
x
)
=
0
{\displaystyle c(x)=0}
olduqda isə Bernulli tənliyinə çevrilir. Rikkati tənliyinin hər hansı
y
1
(
x
)
{\displaystyle y_{1}(x)}
xüsusi həlli məlum olduqda
y
(
x
)
=
y
1
(
x
)
+
z
(
x
)
{\displaystyle y(x)=y_{1}(x)+z(x)}
əvəzləməsi vasitəsilə Bernulli tənliyinə gətirlir. Ümumi halda, Rikkati tənliyi kvadraturaya gətirilə bilmir, yəni həll etmək olmur.
Xüsusi halda:
b
d
x
d
t
=
x
2
+
a
t
α
,
(
∗
∗
)
{\displaystyle b{\frac {dx}{dt}}=x^{2}+at^{\alpha },\quad (**)}
haradakı
α
,
a
,
b
≠
0
{\displaystyle \alpha ,\,a,\,b\neq 0}
—sabiti, ilk dəfə italyan riyaziyyatçısı tədqiq etmişdir Yakopo Françesko Rikkati və ailələrini Bernulli .
α
=
4
n
/
(
1
−
2
n
)
,
n
∈
N
,
{\displaystyle \alpha ={4n}/{(1-2n)},\ n\in \mathbb {N} ,}
или
α
=
−
2
{\displaystyle \alpha =-2}
Jozef Liuvill (1841)isbat etmişdir.
(
∗
)
{\displaystyle (*)}
şəkildə ümumi Rikkati tənliyi ,
(
∗
∗
)
{\displaystyle (**)}
— isə xüsusi Rikkati tənliyi adlanır.
y
′
+
m
(
x
)
(
A
y
+
B
y
2
+
C
)
=
0
{\displaystyle y^{\prime }+m(x)(Ay+By^{2}+C)=0}
olduqda dəyişənlərinə ayrılan,
y
′
+
A
y
x
+
B
(
y
x
)
2
+
C
=
0
{\displaystyle y^{\prime }+A{\frac {y}{x}}+B\left({\frac {y}{x}}\right)^{2}+C=0}
olduqda bircins,
y
′
+
A
y
x
+
B
(
y
)
2
+
C
x
2
=
0
{\displaystyle y^{\prime }+A{\frac {y}{x}}+B(y)^{2}+{\frac {C}{x^{2}}}=0}
olduqda ümumiləşmiş bircns tənliyə çevrilir.
y
′
+
2
y
e
x
−
y
2
=
e
2
x
+
e
x
{\displaystyle y^{\prime }+2ye^{x}-y^{2}=e^{2x}+e^{x}}
Rikkati tənliyini həll edin.
y
1
(
x
)
=
e
x
{\displaystyle y_{1}(x)=e^{x}}
tənliyin həlli olduğunu bilavasitə yoxlamaq olar.
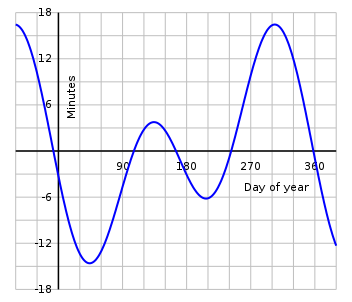
Vaxt tənliyi
Vaxt tənliyi — eyni an üçün verilmiş coğrafi meridianda orta və həqiqi Günəş vaxtlarının fərqidir.
η
=
T
m
−
T
⊙
=
t
m
−
t
⊙
{\displaystyle \eta =T_{m}-T_{\odot }=t_{m}-t_{\odot }}
Vaxt tənliyini əslində vaxt düzəlişi adlandırmaq daha doğru olardı, lakin o tarixi olaraq astronomiyaya vaxt tənliyi kimi daxil olmuşdur.

Vəziyyət tənliyi
Vəziyyət tənliyi - termodinamikanın makroskopik sistemlərini (temperatur, təzyiq, həcm, kimyəvi potensial və s.) bir-biri ilə əlaqələndirən tənlikdir.
f
(
P
,
V
,
T
)
=
0.
{\displaystyle f(P,\;V,\;T)=0.}
U
=
U
(
T
,
V
)
,
{\displaystyle U=U(T,V),}
U
=
U
(
T
,
P
)
,
{\displaystyle U=U(T,P),}
U
=
U
(
V
,
P
)
.
{\displaystyle U=U(V,P).}
U
=
U
(
S
,
V
)
{\displaystyle U=U(S,\;V)}
(daxili enerji üçün kanonik vəziyyət tənliyidir),
H
=
H
(
S
,
P
)
{\displaystyle H=H(S,\;P)}
(entalpiya üçün kanonik vəziyyət tənliyidir),
F
=
F
(
T
,
V
)
{\displaystyle F=F(T,\;V)}
(Helmhots enerjisi üçün kanonik vəziyyət tənliyidir),
G
=
G
(
T
,
P
)
{\displaystyle G=G(T,\;P)}
(Qibbs potensialı üçün kanonik vəziyyət tənliyidir).
Perrot, Pierre (1998). A to Z of Thermodynamics. Oxford University Press. ISBN 0-19-856552-6.
Van der Waals, J. D. (1873). On the Continuity of the Gaseous and Liquid States (doctoral dissertation).

Zelmeyer tənliyi
Zelmeyer tənliyi müəyyən bir şəffaf mühit üçün sınma indeksi və dalğa uzunluğu arasında empirik əlaqədir . Tənlik işığın mühitdə dispersiyasını təyin etmək üçün istifadə olunur.
İlk dəfə 1872-ci ildə Volfqanq Zelmeyer tərəfindən təklif edildi və Augustin Cauchy -nin dispersiyanın modelləşdirilməsi üçün kəşf etdiyi Koşi tənliyinin ümumiləşdirilmiş forması idi.
Orijinal və ən ümumi formada Zelmeyer tənliyi aşağıdakı kimi verilir
n
2
(
λ
)
=
1
+
∑
i
B
i
λ
2
λ
2
−
C
i
{\displaystyle n^{2}(\lambda )=1+\sum _{i}{\frac {B_{i}\lambda ^{2}}{\lambda ^{2}-C_{i}}}}
,
burada n sınma əmsalı, λ dalğa uzunluğu, Bi və Ci isə eksperimental olaraq müəyyən edilmiş Zelmeyer əmsallarıdır . Bu əmsallar adətən mikrometrlərdə λ üçün göstərilir. Qeyd edək ki, bu λ vakuum dalğa uzunluğudur, yəni materialın daxilində olan λ/n formasında deyil. Tənliyin fərqli forması bəzən müəyyən növ materiallar üçün istifadə olunur, məsələn, kristallar.
Cəmin hər həddi,
C
i
{\displaystyle {\sqrt {C_{i}}}}
dalğa uzunluğunda Bi -in absorbsiya rezonansını təmsil edir. Məsələn, BK7 şüşəsi üçün aşağıdakı əmsallar ultrabənövşəyi şüada iki, orta infraqırmızı bölgədə isə bir udma rezonansına uyğun gəlir. Hər bir absorbsiya zirvəsinin yaxınında tənlik n2 = ±∞ qeyri-fiziki qiymətləri verir və bu dalğa uzunluğu bölgələrində Helmholtzun tənliyi kimi daha dəqiq dispersiya modelindən istifadə edilməlidir.

Şredinger tənliyi
Şredinger tənliyi — kvant-mexaniki sistemləri təsvir edən xüsusi törəməli xətti diferensial tənlik; kvant mexanikasının fundamental tənliyi.:1–2 Bu tənlik kvant mexanikasının inkişafında başlıca dönüş nöqtəsi yaratmışdır. Tənlik Ervin Şredingerin adını daşıyır. Şredinger bu tənliyi 1925-ci ildə irəli sürmüş, 1926-cı ildə nəşr etdirmiş, 1933-cü ildə isə bu işinə görə Fizika üzrə Nobel Mükafatı almışdır.
Konseptual olaraq Şredinger tənliyi klassik mexanikadakı Nyutonun ikinci qanununun kvant qarşılığıdır. Bir sıra məlum başlanğıc şərtləri nəzərə aldıqda, Nyutonun ikinci qanunu müəyyən bir fiziki sistemin zamanla hansı yolu keçəcəyinə dair riyazi proqnoz verir. Şredinger tənliyi dalğa funksiyasının zamana görə evolyusiyasını, təcrid olunmuş fiziki sistemin kvant-mexaniki xarakteristikasını ifadə edir. Tənlik zaman-evolyusiya operatorunun unitarlığı şərtindən çıxarıla bilər və buna görə də kvant Hamiltonianı olan özü-özünə qoşma operatorun üstlü qiymətiylə əldə olunmalıdır.
Şredinger tənliyi kvant-mexaniki sistemləri öyrənmək və proqnozlar vermək üçün yeganə yol deyil. Kvant mexanikasının digər formulyasiyalarına Verner Heyzenberq tərəfindən irəli sürülən matris mexanikası və əsası Riçard Feynman tərəfindən hazırlanmış trayektoriya inteqral formulyasiyası daxildir. Pol Dirak matris mexanikasını və Şredinger tənliyini vahid bir formada birləşdirmişdir.

Şrödinger tənliyi
Şredinger tənliyi — kvant-mexaniki sistemləri təsvir edən xüsusi törəməli xətti diferensial tənlik; kvant mexanikasının fundamental tənliyi.:1–2 Bu tənlik kvant mexanikasının inkişafında başlıca dönüş nöqtəsi yaratmışdır. Tənlik Ervin Şredingerin adını daşıyır. Şredinger bu tənliyi 1925-ci ildə irəli sürmüş, 1926-cı ildə nəşr etdirmiş, 1933-cü ildə isə bu işinə görə Fizika üzrə Nobel Mükafatı almışdır.
Konseptual olaraq Şredinger tənliyi klassik mexanikadakı Nyutonun ikinci qanununun kvant qarşılığıdır. Bir sıra məlum başlanğıc şərtləri nəzərə aldıqda, Nyutonun ikinci qanunu müəyyən bir fiziki sistemin zamanla hansı yolu keçəcəyinə dair riyazi proqnoz verir. Şredinger tənliyi dalğa funksiyasının zamana görə evolyusiyasını, təcrid olunmuş fiziki sistemin kvant-mexaniki xarakteristikasını ifadə edir. Tənlik zaman-evolyusiya operatorunun unitarlığı şərtindən çıxarıla bilər və buna görə də kvant Hamiltonianı olan özü-özünə qoşma operatorun üstlü qiymətiylə əldə olunmalıdır.
Şredinger tənliyi kvant-mexaniki sistemləri öyrənmək və proqnozlar vermək üçün yeganə yol deyil. Kvant mexanikasının digər formulyasiyalarına Verner Heyzenberq tərəfindən irəli sürülən matris mexanikası və əsası Riçard Feynman tərəfindən hazırlanmış trayektoriya inteqral formulyasiyası daxildir. Pol Dirak matris mexanikasını və Şredinger tənliyini vahid bir formada birləşdirmişdir.
Biznes Klasteri
Biznes klasteri (ing. business cluster) — xidməti fəaliyyətinin əsasları həmcins olan sahibkarlıq subyektlərinin, təminatçıların və əlaqədar digər təşkilatların xüsusi statusla coğrafi təmərküzləşməsi.
== Tarixi ==
İqtisadçıların aqlomerasiya (təmərküzləşmə) adlandırdığı anlayışın metodoloji tarixi Alfred Marşalın 1890-cı illərdəki tədqiqatlarına qədər gedir. Müasir dövrdə isə "Biznes klasteri" yaxud "Porter klasteri" termini əsasən amerikalı akademik Maykl Porterin 1990-cü ildə nəşr etdirdiyi "Ölkələrin rəqabət üstünlüyü" əsəri ilə təqdim olunmuş və ardınca elmi çevrələr tərəfindən qəbul edilərək məşhurlaşmışdır. İqtisadi proseslərdə müvəffəqiyyətin əldə edilməsində iqtisadiyyatın coğrafi aspektləri isə Paul Kruqmanın "Coğrafiya və ticarət" (1991) əsərində geniş şəkildə işıqlandırılmışdır. Məhz bu cürə tədqiqatlardan sonra biznes klasterləri dövlətlərin iqtisadi strategiyalarında öz yerini almağa başladı.
== Mahiyyəti ==
Maykl Porterə görə müasir qlobal iqtisadi proseslərdə rəqabət üstünlüyü əldə etməyin üsulu kimi bir qisim xüsusi faktorlar əhəmiyyət daşıyır. Məsələn, biznes subyektinin yerləşdiyi məkanın limana yaxın olması yaxud insan resursunun rəqiblərinə nisbətdə daha münasib qiymətlə çalışdırılması kimi nümunələr, xərcləri azaltmaqla rəqabət üstünlüyünü şərtləndirən başlıca amillərdir. Bu qəbildən olan üstünlüyü kortəbii haldan sistemli formaya transformasiya etmək üçün isə müəyyən inzibati tənzimləmərə ehtiyac duyulur. Biznes klasterləri rəqabət anlayışına təsir edən təkmil metodoloji yanaşma kimi məhz bu zərurəti qarşılamaq məqsədi güdür.

Biznes Universiteti
Bakı Biznes Universiteti — 1993-cü ildə yaradılan və Bakı şəhərində fəaliyyət göstərən özəl ali təhsil müəssisəsi.
== Tarixi ==
Bakı Biznes Universiteti 1993-cü ildə təsis edilmişdir. Azərbaycan Respublikası Təhsil Nazirliyi yanında Dövlət Ali Ekspert Komissiyasının 13 mart 1993-cü il tarixli 7/3 saylı qərarı ilə rəsmi qeydiyyata alınaraq institut statusu ilə fəaliyyətə başlamışdır.
== Təhsil ==
Bakalavriat səviyyəsində təhsil müddəti bütün ixtisaslarda 4 il (8 semestr), qiyabi şöbədə isə 5 ildir (10 semestr). Tədris müddətində tələbələrə ixtisasları üzrə əsas və əlavə fənlər tədris olunur.
== Maddi-Texniki bazası ==
Universitetin bütün korpus və köməkçi binaları Yasamal rayonunda, 20 Yanvar və İnşaatçılar metrostansiyalarının arasında yerləşməkdədir. Həmçinin, universitetin kampusunda gəzinti Bağçası, elm parkı, meydan, idman stadionu, oyun meydançası və s. yerləşir.
=== Kitabxana ===
Bakı Biznes Universitetinin kitabxanası var. Burada çox sayda kitablar, dövri nəşrlər, audiovizual və kompüter məlumatı vardır.

Biznes analitikası
Biznes analitikası rəhbər işçilər, menecer və digər korporativ son istifadəçilərə əsaslandırılmış biznes qərarları qəbul etməkdə kömək edən faydalı məlumatların təqdim edilməsi və verilənlərin analizi üçün texnoloji prosesdir. Biznes analitikası analitik nəticələrin alınması üçün operativ işçilərə, qərar qəbul edən korporativ səxslərə əlçatan olan daxili sistem və xarici mənbələrdən məlumatları toplayan, onların təhlilini, həmin verilənlərə sorğuları işləyib hazırlayan və yerinə yetirən, həmçinin hesabat, informasiya paneli, vizual verilənlər yaratmağa imkan verən geniş spektrli alətlər, tətbiqi proqramlar və metodologiyalardan ibarətdir.
Biznes idarəçiliyi
Biznesin idarə edilməsi biznesin idarə olunmasını öyrədən elm sahəsidir. O, biznes əməliyyatlarına nəzarətin bütün aspektlərini əhatə edir. O, həmçinin idarəetmə və liderlik baxımından mühasibat uçotu, maliyyə, layihənin idarə edilməsi və marketinqi əhatə edən sahələri də əhatə edir. Henri Fayol (1841-1925) menecerin bu “funksiyalarını” “idarəetmənin beş elementi” kimi müəyyən etmişdir.

Biznes iqtisadiyyatı
Biznes iqtisadiyyatı — tətbiqi iqtisadiyyatın bir sahəsi olub, iqtisadi nəzəriyyədən və riyazi metodlardan istifadə etməklə müəssisələri, müxtəlif biznes bölmələrinin diversifikasiyasına şərait yaradan faktorları və həmçinin firmaların əmək, kapital və əmtəə bazarları ilə əlaqələrini öyrənir.

Biznes jurnalistikası
Biznes jurnalistikası və ya işgüzar jurnalistika — cəmiyyətlərdə baş verən iqtisadi və maliyyə fəaliyyətlərini və dəyişiklikləri izləyən, qeyd edən, təhlil edən və şərh edən jurnalistikanın bir növüdür. Mövzular iqtisadiyyatla əlaqəli bütün ticari fəaliyyətlərin bütün sahələrini geniş şəkildə əhatə edir. Jurnalistikanın bu sahəsində jurnalistlər, biznesin bütün sahələrində baş verən hadisələr, statistik məlumatlar, valyuta ilə əlaqəli mövzularda xəbərlər və geniş məqalələr təqdim edir. Qəzet, jurnal, radio və televiziya xəbər şoularının əksəriyyətinə biznes seqmenti daxildir. Ətraflı və dərin işgüzar jurnalistika xüsusi olaraq iş və maliyyə jurnalistikasına həsr olunmuş nəşrlərdə, radioda və televiziya kanallarında görünə bilər.
== Tarixi ==
İşgüzar jurnalistika orta əsrlərdən etibarən tanınmış ticarət ailələrinin bir-biri ilə əlaqə yaratdığı dövrdən yaranmağa başladığı güman olunur
XVIII əsrin əvvələrində "Robinson Cruse" əsəri ilə tanınan yazıçı Daniel Defo biznes və iqtisadi xəbərlər yayımlamağa başladı.1882-ci ildə Charles Dow, Edward Jones və Charles Bergstresser Wall Street boyunca bizneslə məşğul olan ailələrin evlərinə telqraf vasitəsilə biznes xəbərlərini çatdırırdılar. Və 1889-cu ildə The Wall Street biznes haqqımda jurnal nəşr etməyə başladı. Dövrünün tanınmış yazar Ida Tarbell özünü bu sahədə jurnalist hesab etməsə də, 1902-ci ildə Standard Oil Co haqqında yazdığı məqalə günümüzdə də istifadə olunan biznes xəbərlərinin formalaşmasına böyük töhfə vermişdir.1990-cı illərdə fond bazarına daha geniş investisiya qoyuluşu ilə işgüzar jurnalistika geniş yayılmışdır. The Wall Street jurnalı, işgüzar jurnalistikanın qabaqcıl nümunələrindən biridir və həm tiraj baxımından həm də orada işləyən jurnalistlərə hörmət baxımından Amerika Birləşmiş Ştatlarının ən yaxşı qəzetlərindən biridir.
== Əhatə dairəsi ==
Biznes jurnalistikası, əksər inkişaf etmiş ölkələrdə geniş yayılsa da , inkişaf etməkdə olan və inkişafdan geri qalmış ölkələrdə çox məhdud bir rola malikdir.
Biznes maqnatı
Maqnat və ya böyük bir iş adamı birdən çox biznesə sahib olmaqla böyük müvəffəqiyyət və böyük sərvət əldə etmiş bir iş adamıdır. Müvəffəqiyyətli sahibkarlar müəyyən bir iş və ya biznes sahəsində böyük təsirə, əhəmiyyətə malik olan biznes mütəxəssislərinə nümunədirlər.
İlk böyük iş adamları John D. Rockefeller, Andrew Carnegie və Henry Ford kimi sənayeçilər idi. Müasir dövrdə Ceff Bezos və Bill Gates kimi texnologiya şirkətlərinin yaradıcıları böyük iş adamlarıdırlar.
Elektron biznes
Elektron biznes və ya e-biznes (en. Electronic business, ru. e-бизнес) — elektron ticarətlə müqayisədə daha geniş anlayış olub, İnternetdə öz veb-saytına, virtual mağazaya, təşkilatın idarıetmə sisteminə, elektron reklamdan istifadəyə, marketinqə, "biznes-biznes" (B2B) və "biznes-istehlakçı" (B2C) modellərinə malikdir.
Elektron-biznes mal və xidmətlərin elektron ticarətini özündə birləşdirir. Elektron biznes mal və xidmətlərin reklamını və hərəkətini, məhsulun bazardakı rəqabətədavamlılığının öyrənilməsini, sifarişin qəbulunu, malın daşınması və çatdırılmasını, istehsalçı və istehlakçı arasında hesablaşmaların həyata keçirilməsini yerləşmə məkanından asılı olmayaraq İnternet şəbəkəsi vasitəsilə həyata keçirir.
== Yaranma səbəbi və xüsusiyyətləri ==
İnformasiya texnologiyaları və sistemlərinin sürətlə inkişafı, şəbəkə texnologiyalarının geniş tətbiqi yeni sahə olan elektron-biznes sahəsinin yaranmasına səbə olmuşdur. Elektron-biznes sahəsi özlüyündə adi biznes sahəsinə aid olan bütün sahələri demək olar ki, əhatə edir. Bu baxımdan artıq fiziki və informasiya məhsullarının satışının, bank, maliyyə, kredit əməliyyatlarının geniş spektrdə elektronlaşdırılması həyata keçirilir. Beləliklə, elektron-biznes əslində ənənəvi biznes proseslərin yeni informasiya texnologiyaları və sistemlərinin, şəbəkə texnologiyalarının. Onların vasitə və imkanlarının aparılması ilə həyata keçirilən prosesdir.
Məhsul (biznes)
'Marketinqdə məhsul' — bazara təqdim edilə bilən və istehlakçıların ehtiyaclarını ödəyəcək bir məhsul və ya xidmət. Məhsullar maddi və qeyri-maddi olaraq bölünür. Sonunculara səyahət agentliyi xidmətləri və ya iş mühasibatı kimi xidmətlər daxildir. Bazarda olan bütün məhsullar təmiz mallardan təmiz xidmətlərə qədər dəyişə bilər. Təmiz xidmətlər, bir məhsulun əldə edilməsini müşayiət edən bütün fayda və satınalmaların əhəmiyyətli bir hissəsi hesab olunur, buna görə də xidmətin inkişafı və əlaqədar rəqabət işin vacib bir hissəsinə çevrilir.
Bir məhsul maddi və ya qeyri -maddi olaraq təsnif edilə bilər. Maddi bir məhsul, bina, nəqliyyat vasitəsi, qadjet və ya geyim kimi toxunmaqla qəbul edilə bilən fiziki bir obyektdir. Qeyri-maddi məhsul, sığorta polisi kimi yalnız dolayı yolla qəbul edilə bilən bir məhsuldur. Xidmətlər geniş şəkildə dayanıqlı və ya qısamüddətli ola biləcək qeyri-maddi məhsullar kimi təsnif edilə bilər.
Sears, Roebuck və Company onlayn məhsul kataloqlarında məhsullarını "şöbələr" olaraq təsnif edir və sonra məhsullarını funksiyası və ya markası ilə potensial müştərilərə təqdim edir.
Şou-biznes
Şou-biznes (ing. Show business) — əyləncə sahəsində kommersiya fəaliyyəti, əyləncə sənayesi.
Aşağıdakılar "şou-biznes" sayılır :
audio və video məhsullar buraxan şirkətlər;
əyləncə sahəsində çalışan artist və bəzi idmançılar;
maliyyə gəliri əldə etməyə üstünlük verən kino, teatr, musiqi, televiziya sahələri.

Biznes logistika
Biznes logistikası — Biznes logistikasının təriflərindən biri "doğru məhsulun lazımi miqdarda və lazımi yerdə, lazımi qiymətə və lazımi vəziyyətdə düzgün müştəriyə çatdırılmasından" danışır. Biznes logistikası bütün sənaye sektorlarını özündə birləşdirir və layihənin həyat dövrlərinin, tədarük zəncirlərinin və nəticədə əldə edilən səmərəliliyin nəticəsini idarə etməyi hədəfləyir.
Biznes logistikası termini 1960-cı illərdən başlayaraq getdikcə qloballaşan təchizat zəncirində müəssisələrin materiallarla təchiz edilməsi və məhsulların göndərilməsinin mürəkkəbliyi səbəbindən inkişaf etmişdir və bu, təchizat zənciri logistikası adlanan mütəxəssislərin çağırılmasına səbəb olmuşdur.
Biznesdə logistikanın mənşə nöqtəsindən istehlak nöqtəsinə qədər materialların axını və saxlanmasını əhatə edən daxili fokus (daxil olan logistika) və ya xarici fokus ola bilər (bax. təchizat zəncirinin idarə edilməsi). İxtisaslı logistikanın əsas funksiyalarına inventarların idarə edilməsi, satınalma, daşınma, anbar, məsləhət və bu fəaliyyətlərin təşkili və planlaşdırılması daxildir. Logistlər təşkilatdakı resursları əlaqələndirmək üçün bu funksiyaların hər biri üzrə peşəkar bilikləri birləşdirirlər.
Logistikanın iki əsas fərqli forması var: biri nəqliyyat əlaqələri və saxlama qovşaqları şəbəkəsi vasitəsilə davamlı material axınını optimallaşdırır, digəri isə hansısa layihəni həyata keçirmək üçün resursların ardıcıllığını əlaqələndirir (məsələn, anbarın yenidən qurulması).
== Paylayıcı şəbəkənin qovşaqları ==
Distribyutor şəbəkəsi istehlakçı və ya sənaye mallarını istehsalçılardan istifadəçiyə çatdırmaq üçün bir neçə vasitəçi tələb edir. Vasitəçilər paylama zamanı məhsulların xərclərini qeyd edərdilər, lakin istehsalçılara nisbətən daha az nəqliyyat xərcləri təmin etməklə istifadəçilərə fayda verirlər.
Biznes turizm
Biznes turizm — həmçinin korporativ turizm (ing. corporate travel) — müxtəlif şirkətlərin işçiləri üçün işgüzar səfərlərin (işgüzar səfərlərin, ing. leisure travel) təşkili və idarə edilməsini təmin edən turizm sənayesinin sahəsi (rekreasiya turizmi ilə yanaşı, ing. business trips).
Korporativ tədbirlər və görüşlər sferası — MICE (ing. Meetings, Incentives, Conferences, Exhibitions) həm də işgüzar turizmlə birbaşa bağlıdır.
== Xüsusiyyətləri ==
Ümumi turizmlə müqayisədə biznes turizmi müxtəlif motivlər və biznes aspektləri tərəfindən qoyulan seçim azadlığına əlavə məhdudiyyətlərlə əhalinin daha kiçik bir hissəsinə çatır. İşgüzar turizm istiqamətləri daha çox biznes məqsədləri üçün əhəmiyyətli dərəcədə inkişaf etdirilmiş ərazilərə çevrilir (şəhərlər, sənaye rayonları və s.). Orta biznes turisti orta turistdən daha zəngindir və daha çox pul xərcləməsi gözlənilir.
Biznes turizmi əsas və ikinci dərəcəli fəaliyyət növlərinə bölünə bilər.